 |
Ultrafast and Doppler-free femtosecond optical ranging based on dispersive frequency-modulated interferometry
Abstract:
An ultrafast and Doppler-free optical ranging system based on dispersive frequency-modulated interferometry is demonstrated. The principle is similar to the conventional frequency-modulated continuouswave interferometry where the range information is derived from the beat frequency between the object signal and the reference signal. However, a passive and static frequency scanning is performed based on the chromatic dispersion of a transform-limited femtosecond pulse in the time domain. We point out that the unbalanced dispersion introduced in the Mach-Zehnder interferometer can be optimized to eliminate the frequency chirp in the temporal interferograms pertaining to the third order dispersion of the allfiber system, if the dynamic range being considered is small. Some negative factors, such as the polarization instability of the femtosecond pulse, the power fluctuation of the optical signal and the nonuniform gain spectrum of the erbium-doped fiber amplifier lead to an obvious envelope deformation of the temporal interferograms from the Gaussian shape. Thus a new data processing method is proposed to guarantee the range resolution. In the experiment, the vibration of a speaker is measured. A range resolution of 1.59 μm is achieved with an exposure time of 394 fs at a sampling rate of 48.6 MHz.
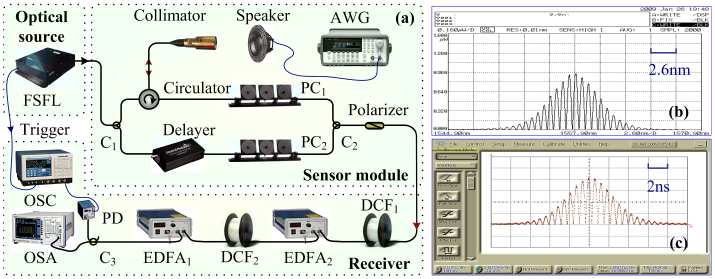
Fig. 1. (a) Schematic of the ultrafast ranging system. FSFL, femtosecond fiber laser; C, fused fiber coupler; AWG, arbitrary waveform generator; PC, polarization controller; DCF, dispersion compensating fiber; EDFA, erbium doped fiber amplifier; PD, photodetector; OSC,oscilloscope; OSA, optical spectrum analyzer. (b) Picture of the spectral interferogram recorded on the OSA (Ando Model AQ6317B). (c) Picture of the temporal interferogram recorded on the OSC (Agilent Model 86116A).
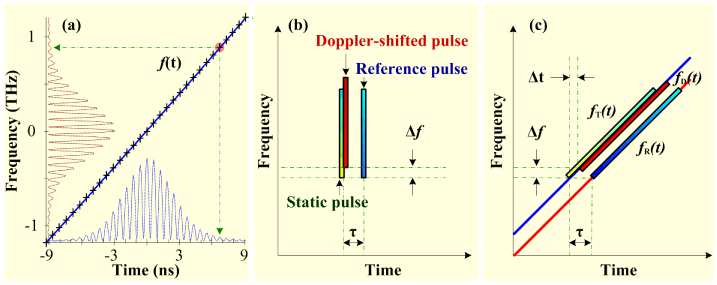
Fig. 2. Visualization of the instantaneous frequency on the frequency-time plane. (a) Time-tofrequency conversion function derived from the temporal and the spectral interferograms. (b) Femtosecond pulses before the dispersion. (c) Femtosecond pulses after the dispersion. To avoid pulse overlap, an offset perpendicular to the time-to-frequency conversion function is introduced between the Dopper-shifted pulse and the static pulse. One should also note that, generally, Doppler shift is very small relative to the optical bandwidth. For clarity, the Doppler shift is magnified in (b) and (c).
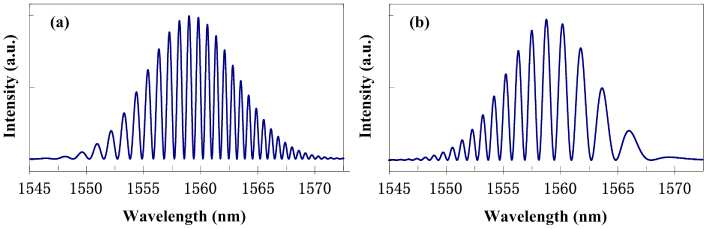
Fig. 3. Linear frequency chirp due to the unbalanced dispersion. (a) Interferogram observed on the OSA when a 6 m length DCF is incorporated in the object arm of the MZI (τ ≈ 10 ps ). (b) Interferogram observed on the OSA when a 6 m length DCF is incorporated in the object arm of the MZI (τ ≈ 8 ps ).
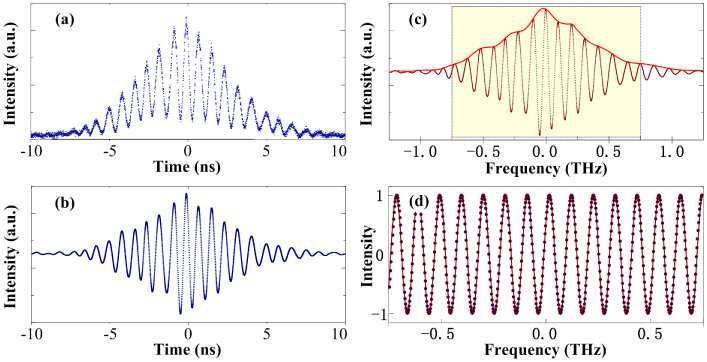
Fig. 4. (a) A typical temporal interferogram (for clarity, 0 τ = 9.65ps is used). (b) Temporal interferogram passing through a band-pass filter. (c) Spectral interferogram transferred from the time domain. (d) Intensity normalized spectral interferogram (dots) and the sine fit result (line).
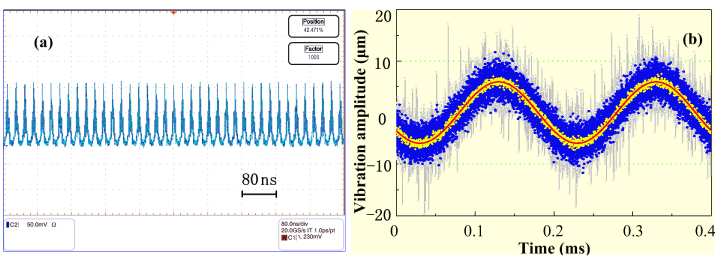
Fig. 5. (a) Picture of the temporal interferograms recorded on the OSC (Tektronix Model TDS7704B, 7 GHz bandwidth, 20 Gs/s sampling speed). (b) Vibration measurement results. Single-shot measurements based on the new data processing method (blue dots). Averaged results (yellow dots). Sine fit result (red line). Single-shot measurements based on the FFT algorithm (light gray region).
